Conduction

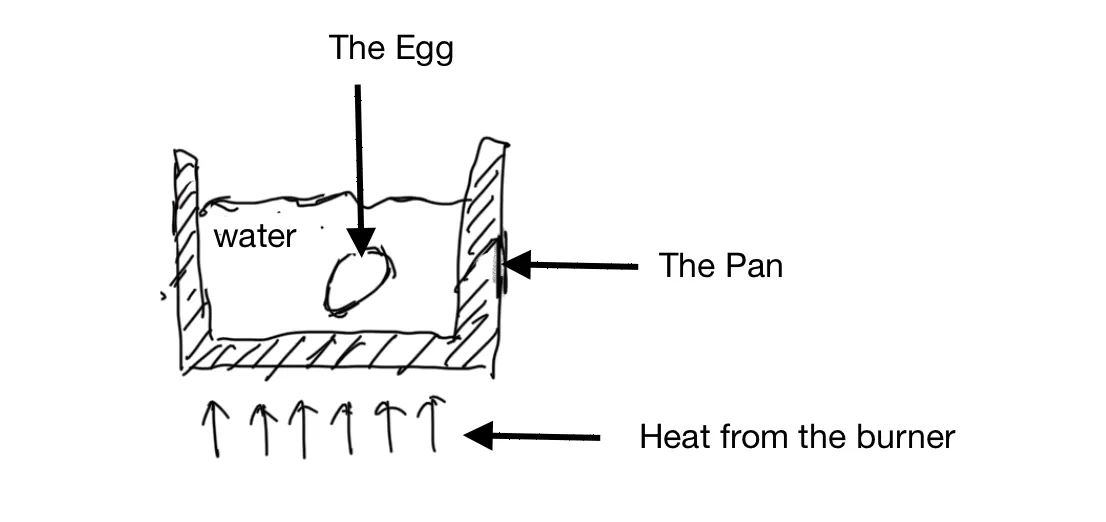
The cooking setup

The above figure shows our cooking setup: the pan conducts the heat from the burner to the water, which covers the egg. A common question from cooks is: what is the best pan? From the perspective of heat, one desired property of a good pan is that it holds its temperature when cold food is added. A substance’s capacity to hold heat is called its specific heat capacity. It measures how much thermal energy it needs to gain or lose for its temperature to rise or fall by 1 degree per unit mass. Cast iron is commonly thought of as retaining heat well, but it actually doesn’t have a particularly high heat capacity (460 J/kg.K). It’s lower than that of stainless steel (490 J/kg.K) and much lower than that of aluminum (910 J/kg.K). But what cast iron lacks in heat capacity, it makes up for in density. So in the same volume, cast iron has more mass and retains more thermal energy than aluminum.

The other desired property of a good pan is that it conducts heat quickly. Conduction follows Fourier's Law. The simplified form of Fourier's Law in one dimension is:

$$q'' = -k {\rm d T \over \rm dx}$$

The heat flux $q''$ (W/m²) is the heat transfer rate in the x-direction per unit area. The thermal conductivity $k$ (W/m.K) is a characteristic of the pan material. The derivative part represents how fast temperature changes over the depth of the pan. Fourier's Law shows that:

1. Heat only flows in the direction of decreasing temperature.
2. Heat flows faster if the rate of change in temperature is greater.
3. Heat flow doesn’t stop until everything is at the same temperature.
4. Specific to conduction: heat transfer rate only depends on the conducting material and the temperatures at the boundaries, and nothing else. If you cannot change either, you cannot change the amount of heat flux by conduction.

But to answer our question of how fast heat transfers, Fourier's Law is missing an important variable: time. Cast iron’s thermal conductivity (55 W/m.K) is higher than that of stainless steel (~40 W/m.K), but we all know that a cast iron pan heats up very slowly. The reason is that some of the heat coming in the hot side doesn’t go out the cold side—it goes to heat up the medium. Per the first law of thermodynamics (conservation of energy), we can write out the energy balance function:

$$Q_{in} - Q_{out} = E_{st}$$

$E_{st}$ is the energy stored in the material over time. It’s determined by the density, specific heat capacity, volume, and how much temperature changes over time. Here we introduce the time variable because all the net energy inflow changes the stored energy, hence the temperature, over time. Combining the energy balance function, Fourier's Law, and a little calculus, we arrive at the heat equation:

$${\partial^2T \over \partial x^2} + {\partial^2T \over \partial y^2} + {\partial^2T \over \partial z^2} = {1 \over \alpha }{\partial^2T \over \partial t^2}$$

Don’t worry about the scary differentials. The left side of the heat equation is about temperature changes over space. The right side of the heat equation is about temperature changes over time. The physical significance of this equation is that the temperature distribution at the beginning determines the temperature distribution over time. The spatial distribution and the temporal distribution are related by $\alpha = k/\rho c_p$. $k$ is the heat conductivity. $\rho$ is the density. $c_p$ is the specific heat capacity. $\alpha$ (mm²/s) is called the thermal diffusivity, which tells us how fast a burst of heat spreads throughout the material. Material with high thermal diffusivity is more responsive to changes in heat input, giving the chef better control. The champion among common pan materials for thermal diffusivity is copper: 114.8 mm²/s.

The solution to the heat equation tells us how temperature changes over time. Fourier’s analytical theory of heat was initially rejected by prominent scientists like Lagrange and Laplace. He was only published after he, searching for the solution to the heat equation, discovered the Fourier transform, which is incidentally also the mathematical foundation of wireless communication. The analytical solution for the heat equation is usually quite complicated. However, it can be shown that, with some assumptions that are valid in normal cooking situations, heat diffusion time is proportional to the square of the depth. It’s a good rule of thumb for estimating cooking time.

Once the heat gets past the pan, it enters the water. This part of the heat transfer path is governed by the law of convection.