Convection

At the top surface of the pan, heat transfers to water by convection. When particles of free-flowing fluid make contact with a surface, they are slowed down. In most cases, it’s valid to assume their speed is 0 at the surface. These particles then slow down the particles in the next layer of fluid. The particles in the next layer, in turn, slow down the particles in the layer above it, and so on and so forth. Eventually, this retardation effect becomes negligible. The region where the fluid speed gradually changes from 0 to the speed of the free-flowing fluid is the velocity boundary layer.

Similarly, the fluid particles that come into contact with the surface achieve thermal equilibrium with the surface. They heat up the particles in the next layer and the next layer. Eventually, a temperature gradient develops in the thermal boundary layer.

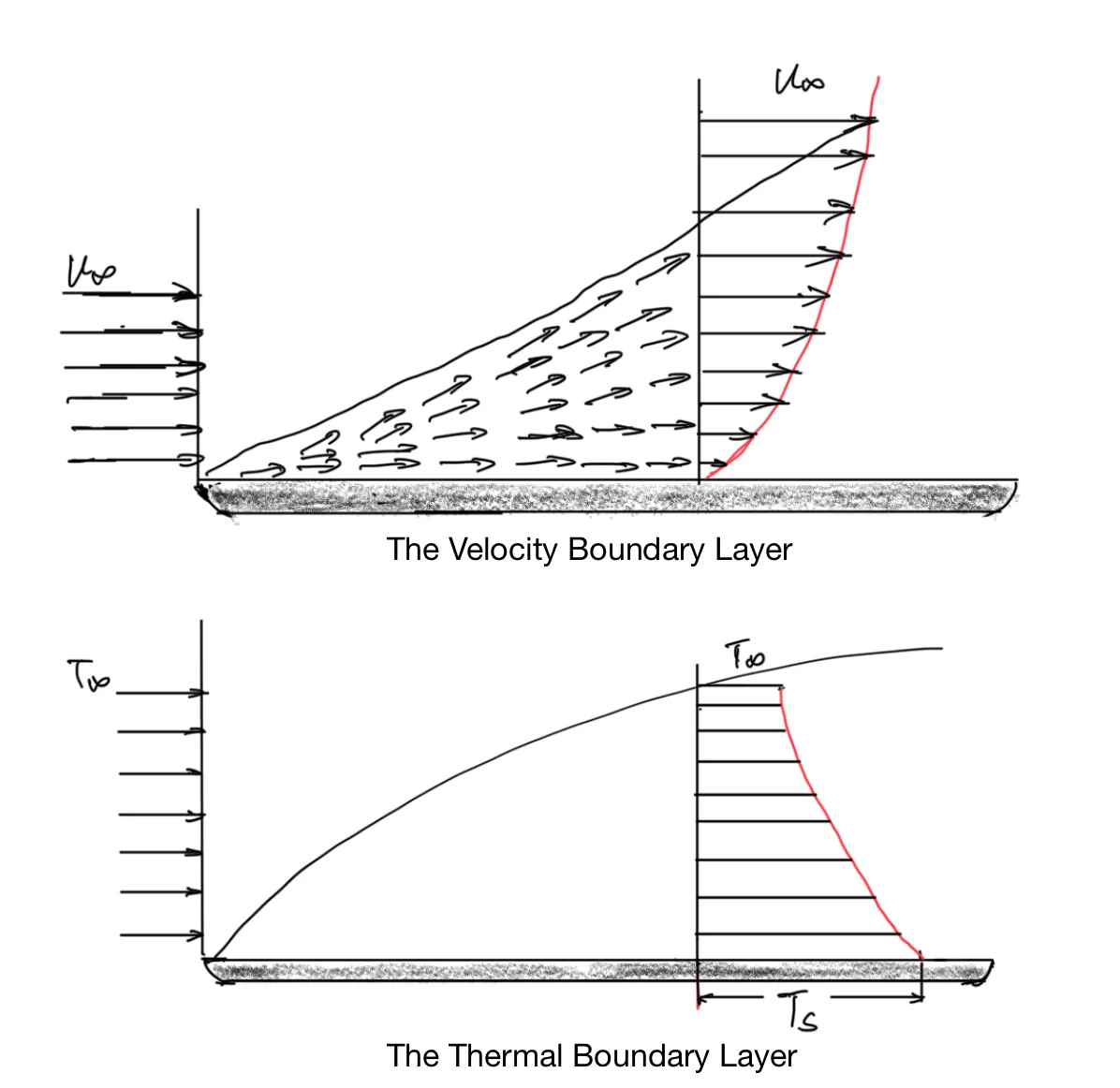
Boundary layer development in convective heat transfer

Assume the temperature at the top surface of the pan is $T_s$, and the temperature of water far from the surface $T_\infty$. Newton’s law of cooling states that:

$$q = h(T_s - T_\infty)$$

$q$ is the heat flux. $h$ is the convective heat transfer coefficient. The heat transfer coefficient is affected by many interdependent variables. The problem of convection is to determine the transfer coefficients.

By the way, this type of equation is quite common in natural phenomena: the rate of change of something is proportional to the difference between two states and a constant characteristic. We saw this in Fourier's law, Ohm’s law, and we will see this in Darcy’s law, which explains how water flows through a bed of coffee grounds.

For the cook, the bad news is that in reality, the flow of fluid near the surface is much more complicated than nicely separated layers. It’s therefore very hard to analyze the boundary layer in cooking liquids. I would say it’s probably not worth it to try. The good news is that, unlike the thermal conductivity coefficient, the chef has some influence over the convective heat transfer coefficient without changing the ingredients. Here are some key insights from the study of convection that we can apply in the kitchen:

1. The faster the fluid flows past the surface, and the more turbulent the flow, the larger the convective coefficient. That’s why blowing on hot food can cool it down.
2. Because of the existence of a velocity gradient, there is bulk fluid motion perpendicular to the surface. This motion is a major contributor to convective heat transfer. In a very thick liquid, there is very little movement, and the velocity boundary layer is not developed. Heat transfers by conduction, not convection. That’s why you need to keep stirring a thick tomato sauce to create forced convection. Otherwise, the bottom will burn while the top is still cold.
3. Liquid has a much bigger convective coefficient than gas. A ratio of 100 to 1 is typical. Most other cookbooks will say here that’s why you can put your hand in a hot oven without getting burned. I will give you a more useful example: if you want to burn a lot of calories, do your exercise in the pool. The convective heat loss from staying in the pool for an hour is greater than the calories you can burn by running on the treadmill for an hour. Another example is that thawing in ice water is much faster than thawing in the fridge air, even though the former is at a lower temperature.

There is one more mode of heat transfer: radiation, the study of which we will leave until the discussion of making toast. Now, let's cook a soft-boiled egg.